Titelbild: xkcd.com

Aufmerksam auf das Thema bin ich durch die Ausschreibung einer Seminararbeit geworden. Aus Urheberrechtlichen Gründen möchte ich meine Ausarbeitung von 2016 nur ausschnitthaft veröffentlichen (für Forschung und Lehre innerhalb eines geschlossenen Personenkreises gelten lockerere Regeln für die Wiedergabe aus Quellen – wenn nicht explizit genehmigt).

Aufbau

1. Einleitung
2. Pseudozufallsgeneratoren vs. Echte Zufallsgeneratoren
3. Pseudozufallsgeneratoren
   1. Kongruenzgeneratoren
   2. Linear rückgekoppelte Schieberegister
   3. Kryptografisch sichere Pseudozufallsgeneratoren
   4. Qualitätstests
4. Physikalische Zufallsgeneratoren
   1. Rauschen als Quelle
   2. Freilaufende Oszillatoren
   3. Chaos und Quanten Zufallsgeneratoren
5. Nachbearbeitung
6. Quellen

Einleitung

Zufallszahlen spielen in vielen Bereichen eine wichtige Rolle. Die wichtigsten Anwendungen liegen in der Kryptographie, sowie in naturwissenschaftlichen und technischen Bereichen, z.B. bei Simulationen. Nicht zuletzt sind Zufallszahlen aber auch bei Gesellschaftsspielen, vom Mensch-ärgere-dich-nicht bis zum Roulette unerlässlich.

Für manche Anwendungsgebiete spielt es eine untergeordnete Rolle, ob sich die Zahlen beim nächsten Programmstart wiederholen, während ein solches Verhalten in der Kryptographie fatale Folgen hätte. Tatsächlich stellt die Kryptographie die höchsten Anforderungen an Zufallszahlen. Dies wird nicht zuletzt dadurch deutlich, dass Zufallsgeneratoren manipuliert werden, um Verschlüsselungen zu schwächen. Von einer solchen Manipulation wird zum Beispiel bei heise berichtet.

Pseudozufallsgeneratoren vs. Echte Zufallsgeneratoren

Pseudozufallszahlen zeichnen sich dadurch aus, dass sie durch einen mathematischen Algorithmus erzeugt werden und somit im eigentlichen Sinne nicht zufällig sind. Sie weisen jedoch ähnliche statistische Eigenschaften wie echte Zufallszahlen auf und eignen sich für die meisten Anwendungen, die Zufallszahlen benötigen. Pseudozufallsgeneratoren sind kostengünstig und schnell, zudem lassen sich ihre Eigenschaften besser analysieren, da sie frei von weiteren Einflüssen sind.

Echte Zufallszahlen lassen sich durch die Beobachtung geeigneter Prozesse erzeugen. Solche Prozesse sind zum Beispiel die Ziehung der Lottozahlen oder das Werfen von Münzen. Diese sind jedoch nicht dazu
geeignet, in kurzer Zeit große Mengen an Zufallszahlen zu generieren. Für die elektronische Generierung von Zufallszahlen wird auf physikalische Prozesse zugegriffen, die zum einen gut erfassbar und zum anderen nicht vorrauszusagbar sind. Dazu zählen unter anderem thermisches Rauschen und bestimmte quantenmechanische Vorgänge. Neben den physikalischen Prinzipien lassen sich auch durch Software echte Zufallszahlen erzeugen. Zwar arbeiten Computer streng deterministisch, aber es lassen sich viele externe Faktoren auswerten, wie Mausbewegungen, Tastatureingaben, Prozessorauslastung und Netzwerktraffic. Diese Methode der Erzeugung wird von modernen Betriebssystemen genutzt. Die Erzeugung von Zufallszahlen in Linux wird in [1] untersucht. Die Datei /dev/random stellt echte Zufallszahlen zur Verfügung, die aus allenEingabegeräte, wie Maus oder Tastatur, Hardware-Interrupts und Zeitvarianzen bei Festplattenzugriffe generiert werden.

Pseudozufallsgeneratoren

Wie bereits erwähnt, erzeugen Pseudozufallsgeneratoren keine Zufallszahlen im eigentlichen Sinne, sondern die Zahlen werden durch eine mathematische Vorschrift gebildet. Diese Zahlen sollen zufällig aussehen, spezielle statistische Eigenschaften haben und in den Anwendungen die gleichen Ergebnisse wie echte Zufallszahlen liefern. Auch die Einsatzgebiete unterscheiden sich nicht. Sie werden bei Simulationen ebenso verwendet, wie in der Kryptographie. Eine Einschränkung wird in [2] und [3] angeführt, es gibt keinen Generator, der in allen Anwendungsfällen die richtigen Ergebnisse liefert. Ursache ist die Abhängigkeit der Zahlen voneinander, welche durch die deterministische Erzeugung entsteht. Die Anwendungen stellen sehr unterschiedliche Anforderungen an die Generatoren. Es ist daher wichtig, die Grenzen der verschiedenen Generatoren zu kennen und für jede Anwendung einen passenden Generator auszuwählen.

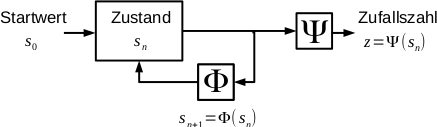
Abbildung 1 zeigt den allgemeinen Aufbau eines Pseudozufallsgenerators. Den Kern eines Generators bildet die Funktion Φ, sie bestimmt maßgeblich das Verhalten. Jedes Mal, wenn die Funktion auf den aktuellen Zustand sn angewendet wird, verändert sich dieser und es entsteht eine neue Zahl. Der Zustand kann entweder direkt ausgegeben werden, oder durch eine Funktion Ψ in veränderter Form. Der Folgezustand kann auch von mehreren Vorgängerzuständen abhängen, dann ist sn+1 = Φ(s n,sn−1 ,…,sn−k ). Durch diese Struktur haben alle Generatoren zwei gemeinsame Eigenschaften:

1. durch den Startwert bzw. die Startwerte werden alle folgenden Werte eindeutig bestimmt
2. abhängig von dem Zustandsspeicher und Φ gibt es periodische Wiederholungen

Kongruenzgeneratoren

Die Klasse der Kongruenzgeneratoren gehört zu den ältesten und am häufigsten verwendeten Pseudozufallsgeneratoren. Sie sind sehr gut erforscht, einfach im Aufbau und schnell. Mit der Darstellung aus Abbildung 1 lassen sich die Generatoren mit den beiden Gleichungen aus Abbildung 2 beschreiben

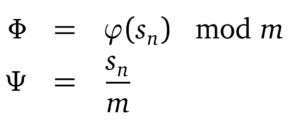
Das zentrale Element der Kongruenzgeneratoren ist die Anwendungen des Modulo auf den Zustand. Dadurch liegen alle Zustände im Intervall [0,m[. Eine Transformation auf das Intervall [0,1[ kann einfach durch Gleichung Ψ erfolgen. Die Funktion φ bestimmt die Art des Kongruenzgenerators.

Der lineare Kongruenzgenerator (LKG) ist der einfachste Kongruenzgenerator. Er wird durch 4 Parameter bestimmt, und hat die Form (Abbildung 3):

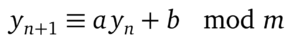
Die Kurzschreibweise ist LKG( m, a, b , y0 ). Exner und Schmitz zeigen in [4], dass folgende Bedingungen hinreichend für eine maximale Periode sind:

1. GGT (b,m) = 1
2. a ≡ 1 mod p für alle Primfaktoren p von m
3. a ≡ 1 mod 4, falls 4 Faktor von m ist

Die Wahl der Parameter ist kritisch, da eine maximale Periode noch keine gute Gleichverteilung garantiert. Ein Problem der linearen Kongruenzgeneratoren ist die Entstehung von Hyperebenen. Hyperebenen sind eine Erweiterung des Begriffes Ebenen aus dem Dreidimensionalen Raum in beliebigen Dimensionen. Für die Analyse werden nicht-überlappende d-Tupel (x1+k ,x2+k ,..,x d+k ) gebildet und deren Verteilung in einem d-Dimensionalen Raum untersucht. Je nach gewählten Parametern zeigen sich die Effekte der Hyperebenen erst ab bestimmten Dimensionen [2].

Neben dem LKG gibt es noch viele weitere Arten von Kongruenzgeneratoren. Sie entstehenden durch leichte Abwandlungen LKG-Struktur. Diese abgewandelten Generatoren können zusätzlich noch kombiniert werden. Ein Beispiel ist der inverse Kongruenzgenerator. Er wird durch die Gleichung aus Abbildung 4 beschrieben:

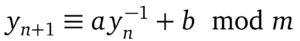
beschrieben.  Hellekalek führt in [2] an, dass sich die Eigenschaften verglichen mit LKGs stark unterscheiden, so weist dieser Typ keine Ausbildung von Hyperebenen auf.

Linear rückgekoppelte Schieberegister

Die einfachste Form, in Hardware Pseudozufallszahlen zu erzeugen sind linear rückgekoppelte Schieberegister (LFSR). Ein Beispiel ist in Abbildung 5 dargestellt.

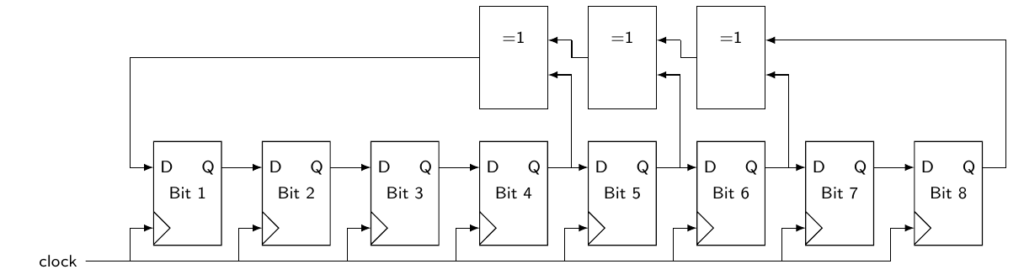
Sie bestehen aus einer Kette von D-Flipflops (D-FF) und einer Rückkopplung über ein, oder mehrere xor Gatter. Der Generator wird durch die Anzahl an D-FFs und den Stellen der xor Gatter vollständig beschrieben. Mathematisch lässt sich diese Struktur durch ein charakteristisches Polynom über einem endlichen Körper mit 2 Elementen ausdrücken (Abbildung 6):

 

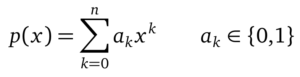
Dabei steht der Exponent k für die Stelle des D-FF und die Koeffizienten ak des Polynoms geben an, welche Stellen für die Rückkopplung genommen werden. Ein LFSR erreicht genau dann Folgen maximaler Länge, wenn das charakteristische Polynom ein primitives Polynom ist. Primitiv bedeutet, dass es sich nicht als Faktor zweier Polynome schreiben lässt, dabei ist zu beachten, dass die LFSR nicht mit reelen Werten arbeitet, sondern mit lediglich zwei Zuständen. Solche Polynome werden nicht algebraisch bestimmt, sondern durch Testen von Computerprogrammen gefunden. Die Ergebnisse stehen in Tabellen zur Verfügung. Neben dem vorgestellten Fibonacci LFSR gibt es noch das Galois LFSR. Bei diesem befinden
sich die xor Gatter zwischen den D-FF und erhalten als jeweils zweiten Eingang das Ausgangssignalletzten. Beide haben aber die gleichen Eigenschaften, auch wenn die erzeugten Folgen unterschiedlich sind. Folgen maximaler Länge weisen besondere statistische Eigenschaften auf [5]. So ist die Anzahl der Nullen und Einsen sehr ausgeglichen, es gibt lediglich eine Eins mehr. Eine weitere Eigenschaft ist das flache, breite Frequenzspektrum.

Kryptografisch sichere Pseudozufallsgeneratoren

Für den Einsatz in der Kryptographie werden Pseudozufallsgeneratoren mit speziellen Eigenschaften benötigt. Es darf nicht möglich sein, aus einer beliebigen Länge an Pseudozufallszahlen auf die nächste Zahl des Generators zu schließen [6, 7]. Diese Eigenschaft wird auch als „next bit test“ bezeichnet und von den bisher vorgestellten Generatoren nicht erfüllt. Pseudozufallsgeneratoren, die diese Eigenschaft erfüllen werden kryptographisch sicher genannt.

Ein Beispiel für solche Pseudozufallsgeneratoren sind Einwegfunktionen, dabei kann – in Bezug auf Abbildung 1 – als Φ ein einfacher Zähler verwendet werden und als Ψ die Einwegfunktion.

Einwegfunktionen sind Funktionen, die aus mathematischer Sicht in eine Richtung leicht zu berechnen sind, deren Umkehrung aber schwer ist. Es wurde bewiesen, dass Einwegfunktionen hinreichend für Erzeugung von Pseudozufallszahlen sind [7]. Einwegfunktionen entstehen durch mathematisch harte Probleme, die sich nur mit sehr viel Aufwand von Computern lösen lassen. Solche Probleme bilden auch die Basis der asymmetrischen Kryptographie. Beispiele sind das diskrete Logarithmusproblem, verwendet im Diffie-Hellmann Schlüsseltausch, oder das Faktorisierungsproblem, welches die Grundlage für RSA bildet.

Ein konkretes Beispiel für einen kryptografisch sicheren Pseudozufallsgenerator ist der Blum-Blum-Shub Generator.

Qualitätstests

Die Qualität von Zufallszahlen, insbesondere der Pseudozufallszahlen, kann mit statistischen Tests bewertet werden. Neben einfachen Tests auf Verteilung, Erwartungswert und Varianz, gibt es Tests auf spezielle Muster und Abhängigkeiten. Das Grundprinzip der Tests besteht darin, die Testergebnisse der zu beurteilenden Zahlen mit den theoretischen Ergebnissen echter Zufallszahlen zu vergleichen. Dazu wird ein χ^2
Anpassungstest durchgeführt. Das Ergebnis unterscheidet prinzipiell in “Test bestanden”und “Test nicht bestanden”. Durch die mehrfache Durchführung eines Tests mit unterschiedlicher Parameterwahl oder der Betrachtung unterschiedlicher Signifikanzniveaus lassen sich aber auch differenziertere Ergebnisse erstellen.

Die Tests auf Verteilung, Varianzen und Erwartungswerte liefern zwar ein Gesamtbild über die allgemeine Verteilung der Zufallszahlen, lassen aber kaum Rückschlüsse auf Abhängigkeiten einzelner Werte zu.
Für die Untersuchung auf Korrelationen sind sehr viele weitere Tests notwendig, da ein Test nur darauf ausgelegt ist, eine Art von Korrelationen zu erkennen. Besteht eine Folge von Zufallszahlen einen Test, so
kann weder eine Aussage getroffen werden, ob eine andere Folge des gleichen Generators den Test auch besteht, noch ob die Zahlen frei von Korrelationen sind. Eine verlässliche Aussage für gute Generatoren kann nur getroffen werden, wenn möglichst viele Tests bestanden werden. Durch diese Eigenschaft wird das Testen von Zufallszahlen sehr aufwändig. Hellekalek gibt in [2] die Anmerkung, dass die Ausführung eines Testes mit verschiedenen Parametern aussagekräftiger ist, als viele Tests mit den Standartparametern.

Die Tests werden daher mit verschiedenen Parametern automatisiert von Software-Suiten ausgeführt. Bekannt sind vor allem DIEHARD Suite und die neuere, verbesserte Software TestU01.

Physikalische Zufallsgeneratoren

Echte Zufallszahlen lassen sich durch die Beobachtung geeigneter physikalischer Prozesse gewinnen, Beispiele sind thermisches Rauschen, radioaktiver Zerfall oder Quanteneffekte. Ein entscheidendes Kriterium für die Generierung von guten Zufallszahlen ist die Unvorhersehbarkeit der zu messenden Größen.

Mario Stipčević und Çetin Kaya Koç gehen in [8] sehr ausführlich auf unterschiedliche Prinzipien physikalischer Zufallsgeneratoren ein und erörtern auf Basis der zugrunde liegenden Gesetzmäßigkeiten die Qualität der Generatoren. So sorgt die zunächst einfach scheinende Bedingung bei näherer Betrachtung für Probleme, denn alle physikalischen Prozesse unterliegen bestimmten Regeln. Viele lassen sich zum Beispiel durch Differentialgleichungen ausdrücken, so dass die gemessenen Werte theoretisch nur von den Startparametern dieser Differentialgleichungen abhängig sind. Prozesse, bei denen weniger Abhängigkeiten bestehen, sind besser zur Erzeugung von Zufallszahlen geeignet. Neben der Eignung des physikalischen Prinzips ist auch die Messung, Auswertung und Weiterverarbeitung im Generator maßgeblich für die Qualität der Zufallszahlen verantwortlich. Fremdeinwirkungen auf den Generator können einen massiven Einfluss auf die Erzeugung und somit auf die Qualität der Zufallszahlen haben, daher sollte ein guter Generator gegen Fremdeinwirkungen geschützt sein. Dieser Aspekt stellt die technische Realisierung vor Herausforderungen, da es zum einen vielfältige Störungsquellen gibt und zum anderen manche Bauteile in einem Alterungsprozess ihre Eigenschaften verändern. Neben den Fremdeinwirkungen gibt es auch statistische Eigenschaften, wie etwa Bauteiltoleranzen bei der Fertigung, welche die Qualität der Zufallszahlen beeinträchtigen können.

In Analogie zu dem in der Kryptographie geltenden Kerckhoffschen Prinzip, bei dem die Sicherheit einer Chiffre nicht auf der Geheimhaltung des Algorithmus beruhen darf, muss ein Zufallsgenerator auch dann gute Zufallszahlen liefern, wenn alle Teile bekannt sind. Die Qualität von Zufallszahlen wird dadurch bestimmt, wie sehr die Zahlen voneinander abhängen. Für die Evaluierung eines Zufallsgenerators werden auch die Qualitätstests der Pseudozufallsgeneratoren benutzt.

Rauschen als Quelle

Der einfachste Ansatz, Zufallszahlen zu erzeugen ist die Auswertung einer Rauschquelle. Zwei viel genutzte, elektrische Rauschquellen sind das thermische Rauschen in Widerständen und ein auf dem Avalanche-Effekt basierendes Rauschen in Halbleitern.

Thermisches Rauschen erzeugt eine sehr kleine Spannung über einen Widerstand. Es entsteht durch die Bewegung von Ladungsträgern bei Temperaturen über dem absoluten Nullpunkt. Um die Spannung zu nutzen muss diese erst verstärkt werden.

Für das Avalanche Rauschen wird eine Zenerdiode, oder der Basis-Emitter Übergang eines Transistors in Sperrrichtung betrieben, sodass ein kleiner Strom fließt. Dabei kommt es immer wieder dazu, dass einige Ladungsträger durch die Sperrschicht tunneln. Dieser Effekt erzeugt messbare Spannungsspitzen. Das Frequenzspektrum entspricht einem pinken Rauschen. Eine hohe Rückwärtsspannung verstärkt den Effekt und sorgt somit für ein Rauschen mit größerer Amplitude. Dies ist ein großer Vorteil gegenüber dem thermischen Rauschen, da die Methode sehr viel unempfindlicher gegen Elektromagnetische Störungen ist.

Nach [8] haben Zufallsgeneratoren, die auf Rauschen basieren haben jedoch einige entscheidende Nachteile, die eine Anwendung in extrem kritischen Bereichen, die perfekte Zufallszahlen benötigen, ausschließen. Ein grundsätzliches Problem liegt darin, dass Rauschen ein allgemeiner Begriff ist, der mehrere physikalische Effekte umfasst. Da diese nicht im einzelnen isoliert werden können, ist ein Beweis über die Zufälligkeit des Rauschens unmöglich. Bei dem thermischen und Avalanche Rauschen kann es zum Beispiel zu Korrelationen kommen, da die Prozesse auf Quantenmechanischen Effekten beruhen. So hängt die momentane Spannung auch ein wenig von dem Stromfluss der Vergangenheit ab und äußere Elektromagnetische Strahlung beeinflusst die Bewegung der Ladungsträger.

Freilaufende Oszillatoren

Ein frei laufender Oszillator (FRO) besteht aus einer ungeraden Anzahl von Invertern, wobei der letzte Inverterausgang an den Eingang des ersten gelegt wird. Wenn der erste Inverter einen Low-Pegel ausgibt, gibt der letzte Inverter ebenfalls einen Low-Pegel aus. An dem Eingang des ersten Inverters liegt somit ein Low-Pegel an und der Inverter ändert seine Ausgabe. Durch die Verzögerungszeiten der Gatter entsteht eine Oszillation. Begünstigt wird die Entstehung einer Oszillation dadurch, dass die Gattereingänge durch ihre digitale Wirkungsweise sehr hohe Verstärkungen haben. Dennoch kann die Phasenverschiebung von exakt 180° dazu führen, dass sich statt der Oszillation ein stabiler Zustand einstellt. Abhilfe schafft ein Verzögerungsglied in der Feedback-Schleife, sodass die Phasenverschiebung leicht von 180° abweicht. Die Frequenz der Osziallation ist sehr Spannungs- und Temperaturabhängig. Elektronisches Rauschen und elektronische Störungen sorgen permanent für minimale kurzfristige Veränderungen der Frequenz, es kommt zu Phasenjitter. Diese Effekte bilden die Grundlage für die Zufallszahlen, je länger der Oszillator läuft, desto mehr addieren sich diese kurzfristigen Schwankungen. Allerdings bleiben sie im Vergleich zur Periode relativ gering.

Ein großes Problem dieser Oszillatoren ist ihre Unstabilität. Sie sorgt zwar erst für Entstehung von Zufall, aber sie lässt die Oszillatoren auch anfällig für Schwingungen aus fremden Quellen werden. Es kann dazu führen, dass die Frequenz ist viel mehr von den externen Einwirkungen geprägt wird, als von den Rauscheffekten. Ursachen für solche Effekte können weitere Oszillatoren in unmittelbarer Nähe sein, oder bewusst geführte Angriffe, wie etwa die Einspeisung einer Frequenz in die Versorgungsspannung [9].

Dieser Typ wird unter anderem in Smartcards verwendet.

Frei laufende Fibonacci Oszillatoren

Dichtl und Dj. Golić stellen in [10] ein neues Konzept für Zufallsgeneratoren vor, in dem sie die Idee linear rückgekoppelte Schieberegister mit frei laufenden Oszillatoren verbinden. Dabei werden die Flipflops aus dem Schieberegister durch Inverter ersetzt. Es wird gezeigt, dass die Zufallsgeneratoren weisen eine wesentlich höhere Entropie aufweisen, weniger störanfällig sind und so implementiert werden können, dass sie energiesparender sind und keine Langzeitkorrelationen aufweisen. Das Ausgangssignal hat sowohl die Eigenschaften eines rückgekoppelten Schieberegisters, als auch eines FLOs. Dadurch entsteht kein Sinussignal, sondern ein chaotisch aussehendes.

Chaos und Quanten Zufallsgeneratoren

Eine weitere Quelle für die Erzeugung von Zufallszahlen ist die Messung von physikalischen, chaotischen Systemen. Solche Systeme sind zwar grundlegend deterministisch und lassen sich durch Differentialgleichungen beschreiben, aber bereits kleinste Änderungen in den Startwerten, oder Einflüsse während des Betriebes sorgen dafür, dass sich der zeitliche Verlauf nicht direkt vorhersagen lässt.
Stipčević und Koç raten in [8] von der Zufallszahlenerzeugung auf Basis des Chaosprinzip ab. Sie geben an, dass sich der Zufall lediglich auf die kleinen Änderungen beschränkt und somit nur wenige Bits umfasst, während die meisten erzeugten Bits deterministisch sind.

Ein besserer Ansatz nach Stipčević und Koç [8] ist die Auswertung von Quanteneffekten. Beispiele für Quanteneffekte, die sich auswerten lassen, sind radioaktiver Zerfall und das Verhalten einzelner Photonen. Bei dem radioaktiven Zerfall lassen sich die genauen Zeitabstände zwischen den Zerfall von zwei Atomen auswerten. Der mittlere Zeitabstand ist zwar sehr stabil, aber die genauen Zeitpunkte des Zerfalls lassen sich nicht vorherbestimmen. Das Grundprinzip der Generatoren besteht darin, zwei Zeitintervalle zu vergleichen. Ist der erste größer, wird eine 0 ausgegeben, ist der zweite größer eine 1. Der Zufallsgenerator setzt sich nach jedem erzeugten Bit in den Ausgangszustand zurück, sodass die generierten Zahlen frei von Korrelationen sind.

Nachbearbeitung

Das Grundprinzip der Nachbearbeitung ist, die vom Generator erzeugten Zufallszahlen durch einen Algorithmus zu verändern und dabei eventuell auf einen Teil der Daten zu verzichten, um Zufallszahlen mit höherer Qualität zu erhalten. Echte Zufallsgeneratoren liefern oft eine nicht ausgeglichene Verteilung von Nullen und Einsen. Diese Schwäche kann bei der Nachbearbeitung behoben werden. Folgende Nachbearbeitungen sind üblich:

• Neumann Korrektur
• kryptographische Hash Funktionen
• Extraktor Funktionen – Extraktor Funktionen sollen aus einer Bitsequenz mit wenig Zufall kürzere Sequenzen mit mehr Zufall erstellen. Ihr Ziel ist es, Alterungsprozesse und andere Einflüsse der Umgebung zu verringen. Die Funktionen sind zustandslos und basieren zum einen auf mathematischen Modellen zur Zufallsquelle und zum anderen auf Hashfunktionen.
• Resilienz Funktionen – Resilienz Funktionen stellen sicher, dass auch bei einer bestimmten Anzahl k deterministischer Bits eine Gleichverteilung von Zufallszahlen erreicht wird. Dabei werden n Bits auf einen Tupel mit m Bits abgebildet. Selbst wenn nur n − k Bits zufällig sind und die anderen in irgendeiner Weise abhängen, sind alle Varianten von m gleich wahrscheinlich. Sie wurden als Nachbearbeitungsschritt für einen Frei laufenden Oszillator entwickelt.

Quellen

[1] Mario Romsy Stephan Müller, Gerald Krummeck. Dokumentation und Analyse des Linux- Pseudozufallszahlengenerators. Technical report, Bundesamtes für Sicherheit in der Informationstechnik (BSI), 2013.

[2] P. Hellekalek. Good random number generators are (not so) easy to find. Mathematics and Computers in Simulation, 46(5-6):485–505, Jun 1998.

[3] Mario Stipčević and Çetin Kaya Koç. True Random Number Generators. Open Problems in Mathematics and Computational Science, page 275–315, 2014.

[4] Helmut Exner and Norbert Schmitz. Zufallszahlen für Simulationen. Münster : Inst. für Math. Statistik d. Westfäl. Wilhelms-Univ., 1982.

[5] https://en.wikipedia.org/wiki/Maximum_length_sequence

[6] Werner Schindler. Evaluation Criteria for Physical Random Number Generators. Cryptographic Engineering, page 25–54, 2008.

[7] Oded Goldreich, Shafi Goldwasser, and Silvio Micali. How to construct random functions. J. ACM, 33(4):792–807, Aug 1986.

[8] Mario Stipčević and Çetin Kaya Koç. True Random Number Generators. Open Problems in Mathematics and Computational Science, page 275–315, 2014.

[9] F. Veljkovic, V. Rozic, and I. Verbauwhede. Low-cost implementations of on-the-fly tests for random number generators. 2012 Design, Automation & Test in Europe Conference & Exhibition (DATE), Mar 2012.

[10} Markus Dichtl and Jovan Dj. Golić. High-Speed True Random Number Generation with Logic Gates Only. Lecture Notes in Computer Science, page 45–62, 2007.