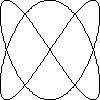
Lissajous-Figuren
Lissajous Figuren spielerisch entdecken…
Geschwindigkeit

| horizontale Frequenz | Offset | (180 entspricht pi) | |
| vertikale Frequenz | Offset |
Geschwindigkeitsfaktor
Was ist das?
Lissajous-Figuren entstehen durch die Überlagerung von zwei Sinuswellen, die senkrecht zueinander stehen.
Benannt sind sie nach dem Mathematiker Jules Antoine Lissajous.
Dieses Skript ist ursprünglich aus purer Lange Weile und der Verfügbarkeit eines alten Computers entstanden,
denn irgendwie macht es Spaß dem roten Punkt hinterherzuschauen 😉 später habe ich es dann erweitert.
Welche Werte sind sinnvoll?
Um die Grundsätzliche Form von Lissajousfiguren zu sehen, ist es erst einmal sinnvoll, eine Frequenz auf 1 zu stellen
und nur ganze Zahlen zu verwenden.
Ein Offset sollte den Wert 0 haben, für die anderen bieten sich die Werte 0,45,90,180 an.
spezielle Formen:
- Frequenzen: 1,0 (gerade Linie), je nach Offset der 0-Frequenz an verschiedenen Stellen)
- Frequenzen: 1,1 bei Offset 90=Kreis (entspricht sin, cos), ansonsten: Ellipse oder Diagonale
Als nächstes kann man mal als Frequenzen 2 ganzzahlige Werte (<10) probieren. Sind die Werte ein ganzzahliges vielfaches voneinander, entstehen wieder die gleichen
Figuren, es läuft nur schneller ab. (Das Skript erkennt das und teilt durch den größten gemeinsamen Teiler)
Wie man gut erkennen sollte, sind die Funktionen immer noch periodisch.
Beispiel:
- hor:2 und 0, vert: 5 und 90 oder 5 und 45
Ob eine Lissajous-Figur periodisch ist, hägt davon ab, ob sich die beiden Frequenzen als Bruch darstellen lassen.
Dabei gilt in etwa, je höher die Zahlen auf dem Bruch, desto näher kommen wir dem unperiodischen Fall. Dieser würde
im Laufe der Zeit den ganzen Bereich ausfüllen.
Um erste Erfahrungen damit zu sammeln, lohnen sich wieder Werte bis 10, diesmal allerdings mit Kommazahlen mit . statt , eingeben
Jetzt fällt auf, dass der rote Punkt irgendwann von der schwarzen Linie abweicht (die auch plätzlich aufhört)
Klickt man auf reset, beginnt die Kurve erneut, wieder auf der schwarzen Linie. (ein ändern der Frequenzen löst keinen! reset aus)
Beispiel:
- hor: 2 und 0, vert: 5.1 und 45 (reset drücken lohnt sich)
Um mehr von der schwarzen Kurve anzeigen zu lassen, muss man die Frequenzen mit der gleichen Zahl multiplizieren.(Am besten mit 10).
Jetzt sollte auch deutlich werden, warum es sich nicht gleich lohnt, hohe Werte einzugeben.
Soviel erstmal zum Crashkurs und nun viel Spaß bei skurillen Zahlen( hohe Zahlen ohne gemeinsamen Teiler) und großen Geschwindigkeiten
Noch etwas für die Musiker: Auch ein Intervall ist ein Verhältnis zwischen zwei Frequenzen und lässt sich so als Lissajous-Figur darstellen.