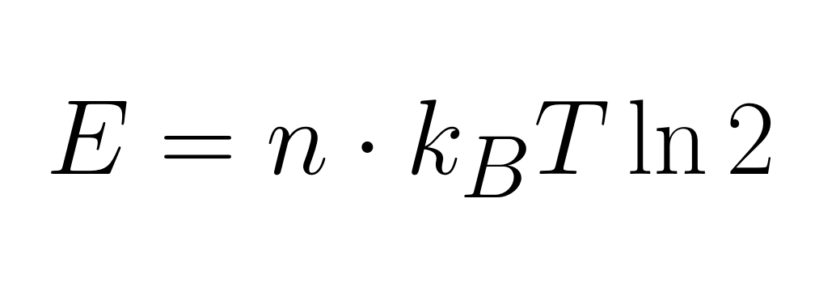Ist Information eine Art von Energie?
Antwort mit einer physikalisch-naturwissenschaftliche Herangehensweise.
Wie genau ich auf die Fragestellung aufmerksam geworden bin, weiß ich nicht mehr – aber sie hat mich so schnell nicht losgelassen. Der folgende Text ist ein Versuch, meine vor zwei Jahren gewonnenen Erkenntnisse festzuhalten und vielleicht etwas dem interessierten Leser weiterzugeben.
Motivation
Die Fragestellung, ob Information physikalisch gesehen eine Art von Energie ist, liefert auch einen Hinweis, ob unser Wissen und Gedanken eine physikalische Bedeutung haben. Auch damit verbunden ist die Frage, ob Informationsverarbeitung – wie z.B. bei einem Computer oder in der Mathematik – grundsätzlich Energie benötigt, oder ob Ergebnisse physikalisch gesehen eher eine wertlose Umformung sind. Dass in der realen Welt Energie benötigt wird, ist offensichtlich, aber wird sogar in der Theorie Energie benötigt?
Grundlagen und Ansatz
Mein erster Ansatzpunkt war der Begriff „Entropie“ in der Informationstheorie, der von Claude Shannon geprägt wurde. Die Entropie gibt dabei den mittleren Informationsgehalt einer Nachricht an. Der Informationsgehalt bestimmt sich dabei dadurch, wie „unerwartet“ bzw. wahrscheinlich ein Ereignis ist. Beispiel: Ein Betrachter bekommt 98 Katzenbilder und 2 Hundebilder. Dann soll er sagen, ob eine Katze oder ein Hund abgebildet ist. Der Informationsgehalt der Aussage: „Es ist eine Katze abgebildet“, ist geringer, als wenn er sagt: „Es ist ein Hund abgebildet“. Das liegt daran, dass es deutlich wahrscheinlicher ist, dass der Betrachter ein Katzenbild hat. Mehr dazu lässt sich hier nachlesen: https://de.wikipedia.org/wiki/Entropie_(Informationstheorie)
Der zweite Ansatzpunkt war, dass es den Begriff „Entropie“ schon in der Thermodynamik gibt und bei Wikipedia stand, dass beide Begriffe miteinander verwandt sind. In der Thermodynamik steht der Begriff Entropie als ein Maß für Unordnung. Je mehr Unordnung besteht, desto weniger lässt sich z.B. voraussagen, wo sich ein Teilchen befindet. Die physikalische Interpretation ist auch: Je höher die Entropie, desto wärmer ist das Teilchen und stärker bewegt es sich. Wärme ist bekanntermaßen eine Form von Energie. Nach dem zweiten Hauptsatz der Thermodynamik ist es nicht möglich, dass Wärme von einem Körper niedriger Temperatur von sich aus auf ein Körper höherer Energie übergeht. Ein Gegenstand kann also wärmer werden (seine Entropie erhöhen), aber nicht von sich aus kälter (Entropie erniedrigen). Also entweder setzt man – wie beim Kühlschrank – Energie ein, um Wärmeenergie zu übertragen und so einen Gegenstand abzukühlen, oder man benötigt eine Umgebung mit weiteren Objekten geringerer Temperatur, auf die ein Teil der Wärmeenergie des Gegenstandes übergehen kann. Eigentlich ist es wie beim Zimmer aufräumen: Nutzt man das Zimmer, ohne aktiv aufzuräumen, wird es mit der Zeit unordentlich. – Das entspricht also völlig den Regeln der Physik. 😉 Zum Aufräumen muss aktiv Energie aufgewandt werden.
Maxwellscher Dämon und Interpretation
Interessanterweise gehen die Ursprünge der Überlegung, ob Information und Energie zusammenhängen auf ein Gedankenexperiment von Maxwell aus dem Jahr 1871 zurück. In diesem Gedankenexperiment – auch genannt Maxwellscher Dämon – wird der zweite Hauptsatz der Thermodynamik in Frage gestellt. Ein „intelligentes Wesen“ (Dämon) kann dabei – unter Idealbedingungen ohne physikalischen Energieaufwand – sich bewegende Teilchen messen und nach ihrer Temperatur separieren. Resultat ist, dass sich ein Teil des Raumes erwärmt, der andere abkühlt. Verschiedene Erklärungsversuche gab es in den folgenden 100 Jahren. Bedeutend ist die Lösung von Leó Szilárd im Jahr 1929, der einen Zusammenhang zwischen Energie und dem Vorgang aus Messung/Information/Speicherung herstellte.
Die heutige Lösung ist, dass einer Information von n-Bit eine Energie E nach folgender Formel zugewiesen werden kann: E = n * kT*ln(2), wobei k die Bolzmannkonstante ist und T die absolute Temperatur des Systems. Das heißt, die Information ist umso mehr wert, je wärmer es ist. Bildlich lässt sich das vielleicht wie folgt wiedergeben:
In einem Zimmer mit niedriger Entropie (hohe Ordnung – thermisch kalt), weiß ich sofort wo etwas ist. Der Informationsgehalt, wo sich ein Gegenstand befindet, ist gering – er ist eben dort, wo er erwartet wird. In einem Zimmer mit hoher Entropie (Unordnung – thermisch heiß) ist das Wissen, wo sich ein Gegenstand befindet, sehr viel wertvoller.
Zudem ergibt sich auch die Interpretationsweise:
Wenn ich einen Gegenstand benötige und weiß, wo er sich befindet – so ist es egal, ob das Zimmer aufgeräumt ist, oder nicht. Das „Chaos beherrschen“ und Aufräumen sind insofern energetisch äquivalente Zustände.
Benötigt Informationsverarbeitung Energie?
Nachdem bekannt ist, dass Information eine Art Energie ist, wird die Fragestellung interessant, inwiefern die Informationsverarbeitung eine Auswirkung auf die Energie hat. Enthält also zum Beispiel die Lösung einer Rechenaufgabe mehr Energie als die Ausgangsbestandteile? Dies würde ja bedeuten, dass die Rechnung an sich ein Prozess ist, der wegen der Energieerhaltung zwingend Energie benötigt. Wie findet Energieumwandlung zu „Informationsenergie“ und von „Informationsenergie“ statt?
Über Literatur zu Quantencomputern (Quantum Computing verstehen, Springer 2015) kam ich zu der Antwort, dass energielose Berechnungen theoretisch möglich sind. Zumindest die Weiterverarbeitung von Information erfordert also nicht zwingend Energie. Das heißt auch, dass der Wirkungsgrad eines Computers in Bezug auf gewonnene Informations-Energie vs. benötigte elektrische Energie Null ist. Voraussetzung ist, dass es sich um einen reversiblen Computer handelt. Weiterhin gibt es sehr unterschiedliche Auffassungen, inwiefern der Maxwellsche Dämon überhaupt auf Computer angewandt werden darf (siehe: Exorcist XIV The Wrath of Maxwell’s Demon, Maxwell’s Demon and the Thermodynamics of Computation).
Landauer, der sich auch mit dem Maxwellschen Dämon auseinander setzte, formulierte 1961 eine Hypothese – das Landauer-Prinzip – die sich mit der Umwandlung von „Informationsenergie“ zu thermischer Energie auseinandersetzt. Demnach wird beim Löschen von Information – entspricht dem zurücksetzen von Bits – die gespeicherte Menge Energie in Form von Wärmeenergie frei. Das Messen wird als Energieneutral angenommen. Das ist jedoch noch nicht der Weisheit letzter Schluss. In einer Beamer-Präsentation fand ich schließlich Formeln, die Energieumwandlung beim Messen und Löschen beschrieben. Das Landauer Prinzip ist dementsprechend nur ein Spezialfall.
Ohne weitere Einblicke in die Physik, evtl noch Quantendynamik, endeten an dieser Stelle meine Recherchen. Dass das Thema auch heute noch spannend ist und Wissenschaftler vor Herausforderungen stellt, beweist eine Vielzahl von Paper, die bis in die aktuelle Zeit reichen.
Quellen
Einige Quellen, die ich dazu gefunden habe:
- Szilard, L. über die Entropieverminderung in einem thermodynamischen System bei Eingriffen intelligenter Wesen (1929) https://doi.org/10.1007/BF01341281
- L. Brillouin – Maxwell’s Demon Cannot Operate: Information and Entropy. I(1950)
- Irreversibility and Heat Generation in the Computing Process (R.Landauer 1961)
- Exorcist XIV: The Wrath of Maxwell’s Demon. Part I. From Maxwell to Szilard John Earman and John D. Norton* (1998)
- EXORCIST XIV: The Wrath of Maxwell’s Demon. Part II. From Szilard to Landauer and Beyond (1999)
- Maxwell’s Demon and the Thermodynamics of Computation (2001) https://doi.org/10.1016/S1355-2198(01)00023-5
- P. Hägele – Was hat Entropie mit Information zu tun? https://www.uni-ulm.de/~phaegele/Vorlesung/Grundlagen_II/_information.pdf
- Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information (TU Berlin, 2012)
- The End of the Thermodynamics of Computation: A No Go Result (2013)
- Does Information Have Mass? (2013) https://doi.org/10.1109/JPROC.2013.2273720